Studio KimHippo :D
[Python / NumPy] 11. NumPy 연습 3 - KNN 본문
필요패키지 로드
# -*- coding : utf-8 -*-
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
sns.set()
rand = np.random.RandomState(42)
데이터생성
# NOTE : 2차원 평면에 임의의 점 10개 추출
x = rand.rand(10, 2)
plt.scatter(x[:,0], x[:,1], s=100)
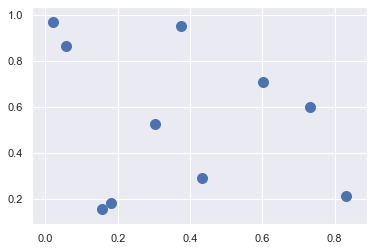
좌표 제곱거리
# NOTE : 각 쌍의 점 사이의 좌표 차이 계산
diff = x[:, np.newaxis, :] - x[np.newaxis, :, :]
diff.shape
# NOTE : 좌표 차이를 제곱함.
sq_diff = diff**2
print(sq_diff.shape)
# NOTE : 제곱 거리를 구하기 위해 좌표 차이를 더함.
dist_sq = sq_diff.sum(-1)
print(dist_sq.shape)
print(dist_sq.diagonal())Out [1] :
(10, 10, 2)
Out [2] :
(10, 10, 2)
(10, 10)
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
가장 가까운 이웃의 인덱스 제공
nearest = np.argsort(dist_sq, axis = 1)
print(nearest) # NOTE : 왼쪽 열이 가장 가까운 이웃의 인덱스 제공
Out [1] :
[[0 3 4 5 8 1 9 7 2 6]
[1 4 6 9 8 0 7 3 2 5]
[2 7 9 8 6 4 3 1 0 5]
[3 5 0 8 4 9 7 2 1 6]
[4 1 0 8 9 6 3 5 7 2]
[5 3 0 8 4 9 1 7 2 6]
[6 1 9 4 8 7 2 0 3 5]
[7 2 9 8 6 4 1 3 0 5]
[8 9 4 7 2 3 0 1 5 6]
[9 8 7 2 6 1 4 0 3 5]]
그래프로 표시
K = 2
nearest_parti = np.argpartition(dist_sq, K + 1, axis = 1)
plt.scatter(x[:, 0], x[:, 1], s=100)
# NOTE : 각 점을 두 개의 가장 가까운 이웃과 선으로 이음.
K = 2
for o_rep in range(x.shape[0]):
for i_rep in nearest_parti[o_rep, : K+1]:
# NOTE : x[o_rep]부터 x[i_rep]까지 선으로 이음.
# NOTE : zip 매직 함수를 이용함.
plt.plot(*zip(x[i_rep], x[o_rep]), color = 'black')

참고
O'REILLY 제이크 밴더플래스 저/ 위키북스 김정인 역 - 파이썬 데이터 사이언스 핸드북
'Python Study > NumPy' 카테고리의 다른 글
| [Python / NumPy] 10. NumPy 연습 2 - 2014년 시애틀 강수량 데이터 활용 (0) | 2019.07.08 |
|---|---|
| [Python / NumPy] 9. NumPy 연습 1 - 미국 대통령 키 데이터 활용 (0) | 2019.07.08 |
| [Python / NumPy] 부록. NumPy 데이터 타입 (0) | 2019.07.08 |
| [Python / NumPy] 8. NumPy의 구조화된 배열 (0) | 2019.07.08 |
| [Python / NumPy] 7.팬시 인덱싱, NumPy 정렬 (0) | 2019.07.08 |
Comments




